美国教育家杜威说过：“教学决不仅仅是一种简单的告诉，教学应该是一种过程的经历，一种体验，一种感悟”。新课标强调以学生发展为本的原则，不再简单机械的传授给学生知识，倡导教师放手把学习的主动权交给学生，努力为学生营造探索的空间，让学生在努力探究中获得知识，发展思维、培养能力，但在教学中也出现了一些片面的做法，把学生探究作为唯一的活力元素，自主探究成为了一种摆设，未能激起学生数学思维的深度参与，未能促进课堂教学目标的高效达成。

此次有感是基于二年级《除法竖式》进行了多次的教学实践而写，下面结合这一内容的三次教学片断，谈一些思考和体会。

案例：

第一次教学片断：

一、学生活动，运用旧知解决问题

（一）呈现题目，明确题意

13根小棒，每4根分一组，结果怎样？

1.出示题目，明确题意。

（二）交流想法，解决问题

13根小棒，每4根分一组，结果怎样？、

问题：结果怎样呢？你是怎么知道的？

学生汇报。

方法一：13÷4＝3（份）……1（根）

方法二：摆一摆。

教师：仔细观察，这位同学先做了什么？（先拿出13根小棒。）

教师：接下来他又做了什么？（有4根就分一份）

教师：分了多少份？是多少根小棒？还剩多少根？（分了3份，一共分走了12根小棒，还剩1根小棒。）

让学生体会：13根小棒，每4根分一份，可以分3份，还剩1根。

教师：摆（圈）的过程和算式的书写过程哪里相同？哪里不同？他们都分别表示什么？

（设计意图：沟通符号表征、图形表征、语言表征之间的关系，体会同一件事可以有不同的表征形式，但含义是相同的。）

二、根据平均分的操作能探究除法竖式的写法，明确竖式中各数的含义。

（一）感受除法竖式的必要性。

教师：刚才有的同学用摆或算的方式，都表达了同一个意思—平均分13根小棒。如果有53根小棒，每4根分一份，能分几份？还剩几根？你想用什么方法来解决呢？（感受用摆、圈的方法的不便，感受除法竖式计算的必要性）

教师：我们需要学习一种新的方法—除法竖式。这个除法算式，我们叫它横式，除法横式还可以写成除法竖式。除法竖式应该怎样写呢？请同学们打开小方格，探究除法竖式的书写方式，一番探究后，学生出现了以下写法： 

                   

……

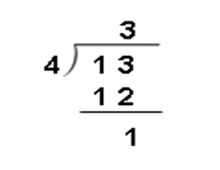
三、尝试练习，进行巩固。

1.完成书本第62页的“做一做”第1题），请你边分边写竖式。

学生独立完成，教师巡视收集典型案例并组织交流汇报。

小结：11除以3，商3，三三得九，减一减，余2.

通过迁移学习表内除法竖式。

教师：如果我们有16根小棒，每4根一组，结果会怎么样呢？请你自己分一分，写一写。

学生活动，教师巡视，了解学生解决问题的基本思路与基本方法，选取典型案例。

教师组织学生讨论如下问题。

（1）   读懂了吗？

（2）   竖式中的两个16表示意思相同吗？它们分别表示什么？

（3）   你发现这道题和我们刚学的有什么相同？有什么不同？

（4）   分完后没有剩余，我们怎么表示？

 

2、巩固表内除法竖式。

完成书本第63页“做一做”第2题）：请同学们自己读题，然后圈一圈，写一写。

学生独立解决问题，教师巡视，了解学生解决问题的情况，选取典型案例并组织交流。

教师：这个竖式表示什么意思？竖式中每个数的含义是什么？

 

三、对比反思，总结全科，积累经验。

教师：通过今天的学习你有什么收获？

教师：除法竖式和除法横式有什么不同？有什么好处？你想对大家说点什么？

 

教学反思：练习检测环节，还是有较多学生出现了错误，比如商的位置错误，竖式书写漏写除数与商的积等。在上述教学过程中，学生经历了自主探究的历程，经过了观察、对比，找到了除法竖式的正确写法，然而一节课下来，还是出现了较多错误，本节课学生还没有接触过除法竖式，就让学生自主探究，没有收到实效，成为了知识负迁移的催化剂。由此引发我们深思：新课标提倡自主、合作、探究的学习方式，是不是所有数学知识都让学生探究得出？是不是该给接受式学习方式予以全盘否定？显然，极端地对任何学习内容都让学生探究，好不犹豫地摒弃接受式学习是不妥当的，如何让学生的探究更恰当、更合理、更深刻，我进行了一定的调整。

第二次教学片断：

教学过程：

一、学生活动，运用旧知解决问题

（一）呈现题目，明确题意

13根小棒，每4根分一组，结果怎样？

问题：

1.出示题目，明确题意。

（三）交流想法，解决问题

学生汇报。

方法一：13÷4＝3（份）……1（根）

方法二：摆一摆。

教师：仔细观察，这位同学先做了什么？（先拿出13根小棒。）

教师：接下来他又做了什么？（有4根就分一份）

教师：分了多少份？是多少根小棒？还剩多少根？（分了3份，一共分走了12根小棒，还剩1根小棒。）

让学生体会：13根小棒，每4根分一份，可以分3份，还剩1根。

教师：摆（圈）的过程和算式的书写过程哪里相同？哪里不同？他们都分别表示什么？

（设计意图：沟通符号表征、图形表征、语言表征之间的关系，体会同一件事可以有不同的表征形式，但含义是相同的。）

二、根据平均分的操作能理解除法竖式的写法，明确竖式中各数的含义。

（一）感受除法竖式的必要性。

教师：刚才有的同学用摆或算的方式，都表达了同一个意思—平均分13根小棒。如果有53根小棒，每4根分一份，能分几份？还剩几根？你想用什么方法来解决呢？（感受用摆、圈的方法的不便，感受除法竖式计算的必要性）

教师：我们需要学习一种新的方法—除法竖式。这个除法算式，我们叫它横式，除法横式还可以写成除法竖式。

13根小棒，每4根分一组，结果怎样？

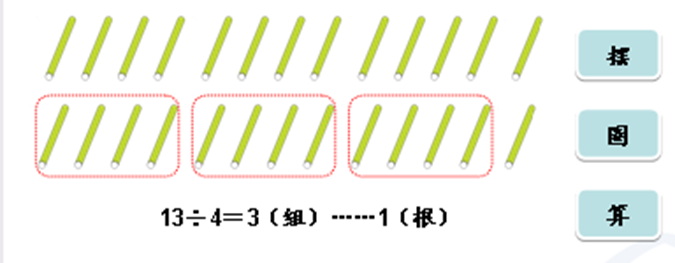
二、研讨竖式，理解各部分含义

教师出示图，这就是除法竖式。（板书课题：除法竖式）

看看这个除法竖式，竖式中的每个数都有名字，你知道他们都叫什么吗？                    

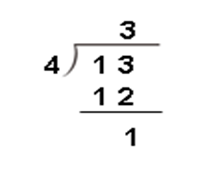
2、沟通平均分操作与书写竖式之间的关系，理解竖式中每个数的含义。

（1）建立联系。

教师：知道每个数的名称，知道竖式中每个数分别表示什么意思吗？

教师：看来这对大家有些难度，下面我们就对照平均分小棒的操作过程，一边分小棒，一边写一写除法竖式。请大家跟老师一起边分，边写，边说。

（2）沟通关系。

教师：先写被除数13（要分的13根小棒），再写除号，（板书），表示（平均分）。

再写除数4（每4根一份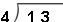），表示什么意思？（13根小棒，每4根分一份。）

教师：请你按要求把13根小棒，每4根分一份，再重新分一分。

教师：结果可以分成3组，这个“3“写在哪里？

教师：为什么要写在个位上？（板书：。）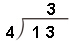

教师：谁能完整地说一说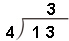表示什么意思？（13根小棒，每4根分一份，可以分3份）

教师：谁能边分边说竖式中每个含义的意思？

教师：要分13根小棒，现在已经分掉了多少根？你从哪里知道分掉了12根？

使学生体会：从图中我们可以看到一组有4根，有这样的3组，3个4是12根小棒。从算式中我们可以用商乘除数3×4的积是12。

教师：这个“12“写在哪里？表示什么意思？它是怎样计算出来的？（12。）

教师：我们画一条横线表示按要求分了一次。（板书：。）

教师：这条横线表示什么？

教师：要分13根小棒，已经分掉了12根小棒，还剩多少根？你是怎么知道的？）

使学生体会：从图中我们还可以看到还剩下1根，从算式中我们可以用要分的13根减去已经分掉的12根，还剩1根。

教师：这个“1”写在哪里？表示什么意思？

教师：它是怎么算出来的？（补充板书：1。）

3、回顾对比，理清写法。

教师：我们一边分小棒一边写出了除法竖式。请同学们认真地想一想，我们是怎样分小棒的？又是怎样写竖式的？竖式中的每个数表示什么意思？想完后和同学说一说。

教师：前面我们学习了有余数除法算式的口算方法，今天又学习了有余数除法的竖式，你觉得这两种方法有什么相同方法？有什么不同的地方？

（设计意图：本环节重点帮助学生建立分小棒的过程与写除法竖式之间的联系。通过边分小棒边写竖式这种对应的学习过程，帮助学生在直观操作的基础上理解竖式中每个数的含义，回顾对比横竖式，加深对有余数除法的不同表征形式的理解。）

4、尝试练习，进行巩固。

完成书本第62页的“做一做”第1题），请你边分边写竖式。

学生独立完成，教师巡视收集典型案例并组织交流汇报。

小结：11除以3，商3，三三得九，减一减，余2.

5、通过迁移学习表内除法竖式。

教师：如果我们有16根小棒，每4根一组，结果会怎么样呢？请你自己分一分，写一写。

学生活动，教师巡视，了解学生解决问题的基本思路与基本方法，选取典型案例。

教师组织学生讨论如下问题。

（1）   读懂了吗？

（2）   竖式中的两个16表示意思相同吗？它们分别表示什么？

（3）   你发现这道题和我们刚学的有什么相同？有什么不同？

（4）   分完后没有剩余，我们怎么表示？

6、巩固表内除法竖式。

完成书本第63页“做一做”第2题）：请同学们自己读题，然后圈一圈，写一写。

学生独立解决问题，教师巡视，了解学生解决问题的情况，选取典型案例并组织交流。

教师：这个竖式表示什么意思？竖式中每个数的含义是什么？

三、对比反思，总结全科，积累经验。

教师：通过今天的学习你有什么收获？

教师：除法竖式和除法横式有什么不同？有什么好处？你想对大家说点什么？

教学反思：

第二次教学通过“直观或操作—算式—竖式”，在教学过程中加强了对算理的理解，体现了知识的形成过程，并体现了不同表征方式的相互转换，并进行了有针对性的突破，突出了商的书写位置，使学生理解了除法竖式的含义，掌握了除法竖式的写法，但是整个过程教学过程中学生始终处于模仿的阶段，不需要太多的思考，学生缺乏探究学习，思维得不到发展，切断了学生积极探究，主动获取知识的机会，如何让学生去探究，让学生的数学思维得到进一步得到提升还有待探究。课后学校专家和老师们对本节课进行了研讨，笔者认为数学计算课应让学生有所体验、感悟和发展，关注学生数学思维的发展，基于以上思考，我们对教案进行了修改，进行了第三次的试教。

第三次教学片断：

一、学生活动，运用旧知解决问题

（一）呈现题目，明确题意

13根小棒，每4根分一组，结果怎样？

问题：

1.出示题目，明确题意。

（二）交流想法，解决问题

学生汇报，呈现算法。

引导学生说想的过程，教师板书：

 13÷4＝3（份）……1（根）

 想：（         ）×4=12 

   13-（ 12   ）=1

师：这种算法比较麻烦，我们可以用除法竖式来表示：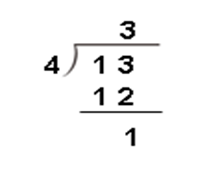

（设计意图：教师通过学生思考和探究，将旧知迁移到新知，沟通了除法横式和除法竖式之间的关系）

2．对比“除法口算思路”和“除法竖式”，感受除法竖式产生的必要性。

（设计意图：沟通符号表征、图形表征、语言表征之间的关系，体会同一件事可以有不同的表征形式，但含义是相同的。）

3.尝试练习，巩固写法。

16÷3=       15÷4=

学生汇报，强调商的书写位置，突出商的位置。

二、在计算中理解除法竖式的写法，明确竖式中各数的含义。

1．看看这个除法竖式，竖式中的每个数都有名字，你知道他们都叫什么吗？                   

2、沟通平均分操作与书写竖式之间的关系，理解竖式中每个数的含义。

（1）建立联系。

（2）沟通关系。

3、回顾对比，理清写法。

4、尝试练习，进行巩固。

完成书本第62页的“做一做”第1题），请你边分边写竖式。

学生独立完成，教师巡视收集典型案例并组织交流汇报。

5、通过迁移学习表内除法竖式。

教师：如果我们有16根小棒，每4根一组，结果会怎么样呢？请你自己分一分，写一写。

学生活动，教师巡视，了解学生解决问题的基本思路与基本方法，选取典型案例。

6、巩固表内除法竖式。

完成书本第63页“做一做”第2题）：请同学们自己读题，然后圈一圈，写一写。

学生独立解决问题，教师巡视，了解学生解决问题的情况，选取典型案例并组织交流。

教师：这个竖式表示什么意思？竖式中每个数的含义是什么？

三、对比反思，总结全科，积累经验。

教师：通过今天的学习你有什么收获？

教师：除法竖式和除法横式有什么不同？有什么好处？你想对大家说点什么？

课后反思：

在计算教学中，直观操作和除法口算是学生进行积极思维的重要手段，在教学中，教师以学生口算思考过程为突破口，教师鼓励学生口算，通过学生描述思考过程，将旧知迁移到新知，让学生在整个过程中，让学生通过想、算、思、说的过程，让学生明确计算过程的算理和算法，学生学习数学的任何内容都应该培养学生有条理、有根据地进行思维活动，学生的对除法竖式的认识从模糊到清晰，学生不光初步掌握的除法竖式的算理和算法，而且有了一定的数学思考。

【对比反思】

（一）以合理的结构和不同表征方式的转换，加强学生对运算意义的理解。通过开放性的操作活动，让学生在对比中实现从直观到抽象，从口算到笔算的转移，为学生选择算法的依据做好充分的准备。

（二）重视在探索的过程中加强对算理的理解，体现知识的形成过程。在操作的基础上呈现学生的求商方法，再利用直观图，承接除法口算思路给出除法竖式，将直观图、除法横式和除法竖式联系起来，进而理解除法竖式的算理，及各部分联系。这样的探索过程，由直观到抽象，便于学生深刻理解除法竖式的算理，初步形成除法竖式。

（三）注重体验感悟，给学生提供有效的科学的探究载体，引领学生探究，通过载体帮助学生寻求学习新知的最近发展区域，主动获取知识，尝到成功的喜悦。在最后的教学过程中教师并没有直接呈现除法竖式各部分名称和意义，而是让学生在不断的探究、摸索和对比中感悟除法竖式。掌握除法竖式的算理和算法。循序渐进，对学生“四能”的培养被细致的体现了出来，在教学时即有“抓手”，也合乎学生思维发展特点，在教学中让学生体会除法竖式的意义，避免了生硬的模仿。